Multi-Touch Attribution (MTA) to zaawansowane podejście w analityce marketingu cyfrowego, które przypisuje wartość każdemu punktowi styku, z którym konsument wchodzi w interakcję podczas swojej podróży do konwersji. W przeciwieństwie do tradycyjnych modeli, które przypisują sukces konwersji pojedynczemu punktowi styku, MTA rozpoznaje złożoność zachowań konsumentów, analizując, w jaki sposób różne kanały i interakcje przyczyniają się do ostatecznego wyniku. Metoda ta ma coraz większe znaczenie w wielokanałowym marketingu, ponieważ zapewnia dokładniejszy wgląd w skuteczność różnych strategii i kampanii marketingowych.
W sferze technicznej MTA wykorzystuje algorytmy i metody statystyczne do rozdzielania zasług za konwersję na wiele interakcji z klientami, od pierwszej ekspozycji do ostatecznej akcji konwersji. W tym artykule zamierzamy zbadać niektóre z tradycyjnych i zaawansowanych modeli atrybucji wielodotykowej oraz stojące za nimi algorytmy.
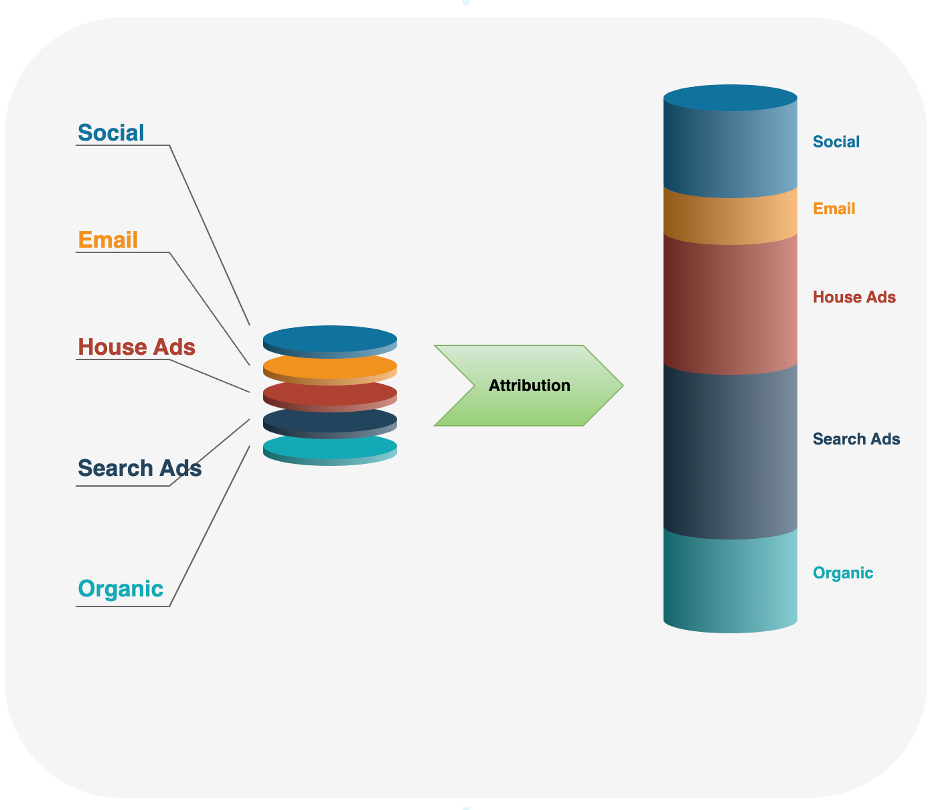
Rysunek 1: Model atrybucji przypisuje wagi do każdego kanału
Modele tradycyjne
Proszę założyć, że mamy serię n punktów styku prowadzących do konwersji i proszę pozwolić C reprezentują całkowitą wartość konwersji. Wartość wkładu przypisana do każdego punktu styku i będzie oznaczane jako Vi. Poniżej przedstawiono różne tradycyjne modele atrybucji
- Atrybucja ostatniego kliknięcia przypisuje pełną wartość konwersji do ostatniego punktu kontaktu przed zakupem. Chociaż jest to proste, jego główną wadą jest lekceważenie wszystkich poprzedzających interakcji z klientem, co potencjalnie nie docenia znaczenia wczesnego zaangażowania i inicjatyw uświadamiających w lejku marketingowym.

- Atrybucja za pierwszym kliknięciem przypisuje początkową interakcję w podróży klienta do całej konwersji. Podejście to pomija wkład kolejnych punktów styku, co często skutkuje wypaczonym zrozumieniem skuteczności strategii w połowie ścieżki i strategii zamykania.

- Atrybucja liniowa równomiernie rozkłada zasługi na wszystkie punkty styku. Jednak krytycznym ograniczeniem tego modelu jest brak uwzględnienia zróżnicowanego wpływu różnych interakcji, co potencjalnie nadmiernie upraszcza wpływ każdego działania marketingowego. Kredyt jest równomiernie rozłożony na wszystkie punkty styku.

- Atrybucja oparta na pozycji (w kształcie litery U) kładzie nacisk na pierwszą i ostatnią interakcję (zwykle po 40%), a reszta jest rozłożona na inne punkty styku. Model ten może niedokładnie uchwycić znaczenie działań w połowie ścieżki i może nadmiernie upraszczać złożone podróże klientów. Większość kredytów trafia do pierwszego i ostatniego punktu styku, a reszta jest równomiernie rozłożona na środkowe punkty styku.

- Atrybucja w kształcie litery W: Rozszerzenie modelu w kształcie litery U, nadaje również dodatkową wagę środkowemu punktowi styku (zazwyczaj konwersji leada), wraz z pierwszym i ostatnim punktem styku.
Te tradycyjne modele atrybucji, choć zapewniają podstawowe ramy dla zrozumienia wpływu marketingu, często nie odzwierciedlają dokładnie skomplikowanego, wieloaspektowego charakteru nowoczesnych podróży konsumenckich. Mają one tendencję do nadmiernego upraszczania procesu lub stronniczości niektórych punktów styku, co prowadzi do potencjalnie wypaczonych spostrzeżeń i decyzji marketingowych. W miarę ewolucji cyfrowego krajobrazu, bardziej wyrafinowane i zniuansowane podejścia, takie jak Multi-Touch Attribution, zyskują na znaczeniu, aby zaradzić tym ograniczeniom.
Modele zaawansowane
Model atrybucji rozpadu czasowego
Time Decay Attribution Model to popularna metoda stosowana w analityce marketingowej do przypisywania konwersji na podstawie czasu punktów styku z klientem. Model ten działa w oparciu o zasadę, że punkty styku bliższe w czasie do konwersji mają większy wpływ niż wcześniejsze.
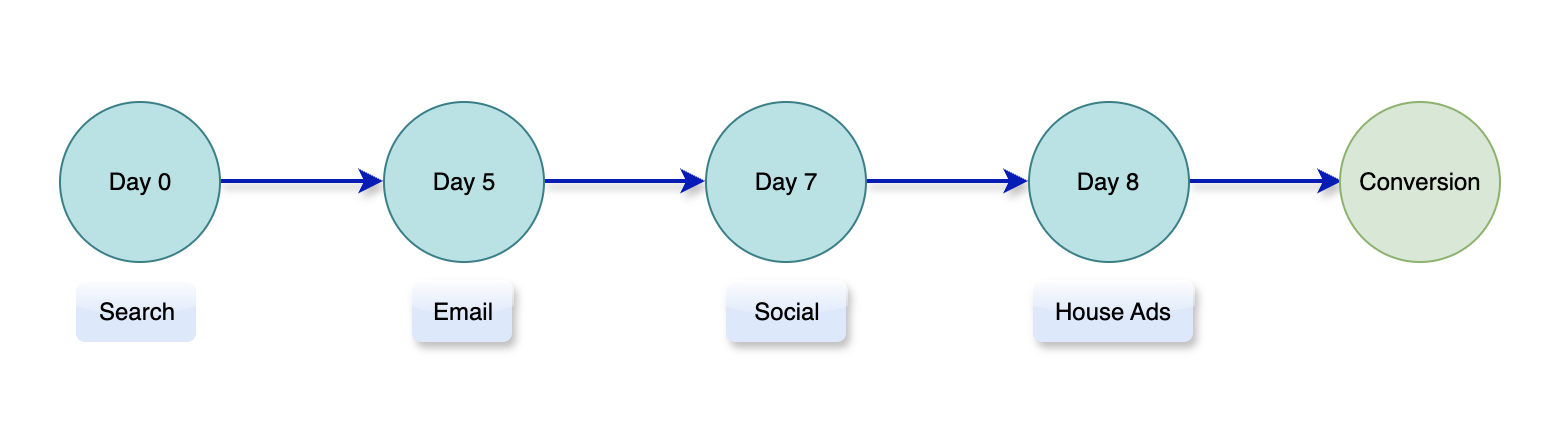
Koncepcja
Model Time Decay przypisuje większą wartość interakcjom marketingowym, które mają miejsce bliżej czasu konwersji. Opiera się on na założeniu, że te późniejsze interakcje mają prawdopodobnie większy wpływ na ostateczną decyzję klienta. Jest to szczególnie przydatne w długich cyklach sprzedaży, w których wiele punktów styku występuje przez dłuższy czas, umożliwiając marketerom ważenie ostatnich interakcji w większym stopniu.
Podejście
- Identyfikacja punktu styku: Identyfikowane są wszystkie punkty styku na ścieżce klienta, od pierwszej interakcji do konwersji.
- Ważenie na podstawie czasu: Każdemu punktowi styku przypisywana jest waga, która rośnie wraz ze zbliżaniem się do zdarzenia konwersji. Waga jest zwykle zgodna z funkcją wykładniczą lub logarytmiczną, w której wzrost przydziału kredytów przyspiesza, gdy punkt styku zbliża się do momentu konwersji.
- Alokacja kredytu: Model oblicza przypisanie, rozdzielając całkowitą wartość konwersji między punkty styku, w oparciu o przypisane im wagi.
Powszechnym podejściem do reprezentowania modelu Time Decay jest funkcja rozkładu wykładniczego. Jeśli t reprezentuje czas punktu styku, a T to czas konwersji, waga W przypisanego do punktu styku można wyrazić jako:
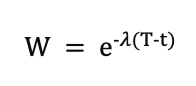
Gdzie:
- e jest podstawą logarytmu naturalnego.
- λ jest stałą szybkości rozpadu, która określa, jak szybko waga punktu styku zmniejsza się w czasie. Wyższa λ oznacza szybszy rozpad.
Modele atrybucji łańcucha Markowa
Model łańcucha Markowa w MTA jest zaawansowaną metodą wykorzystywaną do oceny skuteczności różnych marketingowych punktów styku w podróży klienta. W MTA model łańcucha Markowa traktuje podróż klienta jako sekwencję stanów odpowiadających różnym punktom styku. Kluczową właściwością łańcucha Markowa jest to, że prawdopodobieństwo przejścia do następnego stanu zależy tylko od bieżącego stanu, a nie od poprzednich stanów. Każdy punkt styku w podróży klienta jest stanem w łańcuchu Markowa. Model analizuje przejścia między tymi stanami, aby zrozumieć, w jaki sposób klienci przechodzą przez ścieżkę sprzedaży i jak każdy punkt styku wpływa na ich podróż w kierunku konwersji.
Kontekst
Łańcuchy Markowa zostały opracowane przez Andreya Markova na początku XX wieku. Ich zastosowanie w atrybucji marketingowej jest stosunkowo niedawną innowacją, wykorzystującą ich zdolność do modelowania złożonych, nieliniowych podróży klientów. Wykorzystanie łańcuchów Markowa w atrybucji marketingowej stało się widoczne wraz z rozwojem wielokanałowych strategii marketingu cyfrowego. W środowisku, w którym klienci wchodzą w interakcje z wieloma marketingowymi punktami styku w różnych kanałach przed konwersją, tradycyjne modele atrybucji, takie jak ostatnie kliknięcie lub pierwsze kliknięcie, stały się niewystarczające. Modele łańcuchów Markowa oferowały bardziej dynamiczny i holistyczny obraz.
Podejście algorytmiczne
- Definiowanie stanów: Każdy unikalny punkt styku, wraz z początkiem, konwersją i brakiem konwersji, jest definiowany jako stan.
- Macierz prawdopodobieństwa przejścia: Proszę skonstruować macierz przedstawiającą prawdopodobieństwo przejścia z jednego stanu (punktu styku) do drugiego na podstawie danych historycznych.
- Budowanie łańcucha: Proszę użyć prawdopodobieństwa przejścia, aby zamodelować podróż klienta jako łańcuch Markowa.
- Obliczanie prawdopodobieństwa konwersji: Proszę obliczyć prawdopodobieństwo osiągnięcia stanu konwersji z każdego punktu styku.
- Ocena wpływu punktu styku: Proszę przeanalizować wpływ usunięcia poszczególnych punktów styku na ogólne prawdopodobieństwo konwersji, wskazując ich wkład w podróż.
Poniższa tabela przedstawia podróż czterech klientów i ich współczynnik konwersji.
| Klient | Kanał | Konwersja |
| A | Email ->Ogłoszenia Dom | Nie |
| B | Ogłoszenia w wyszukiwarce -> Ogłoszenia w domu | Tak |
| C | House Ads | Nie |
| D | Reklamy w wyszukiwarce -> Społecznościowe | Tak |
Podróż klienta w powyższej tabeli można zwizualizować jako skierowany graf acykliczny (DAG) z prawdopodobieństwem dla każdego przejścia, jak poniżej.
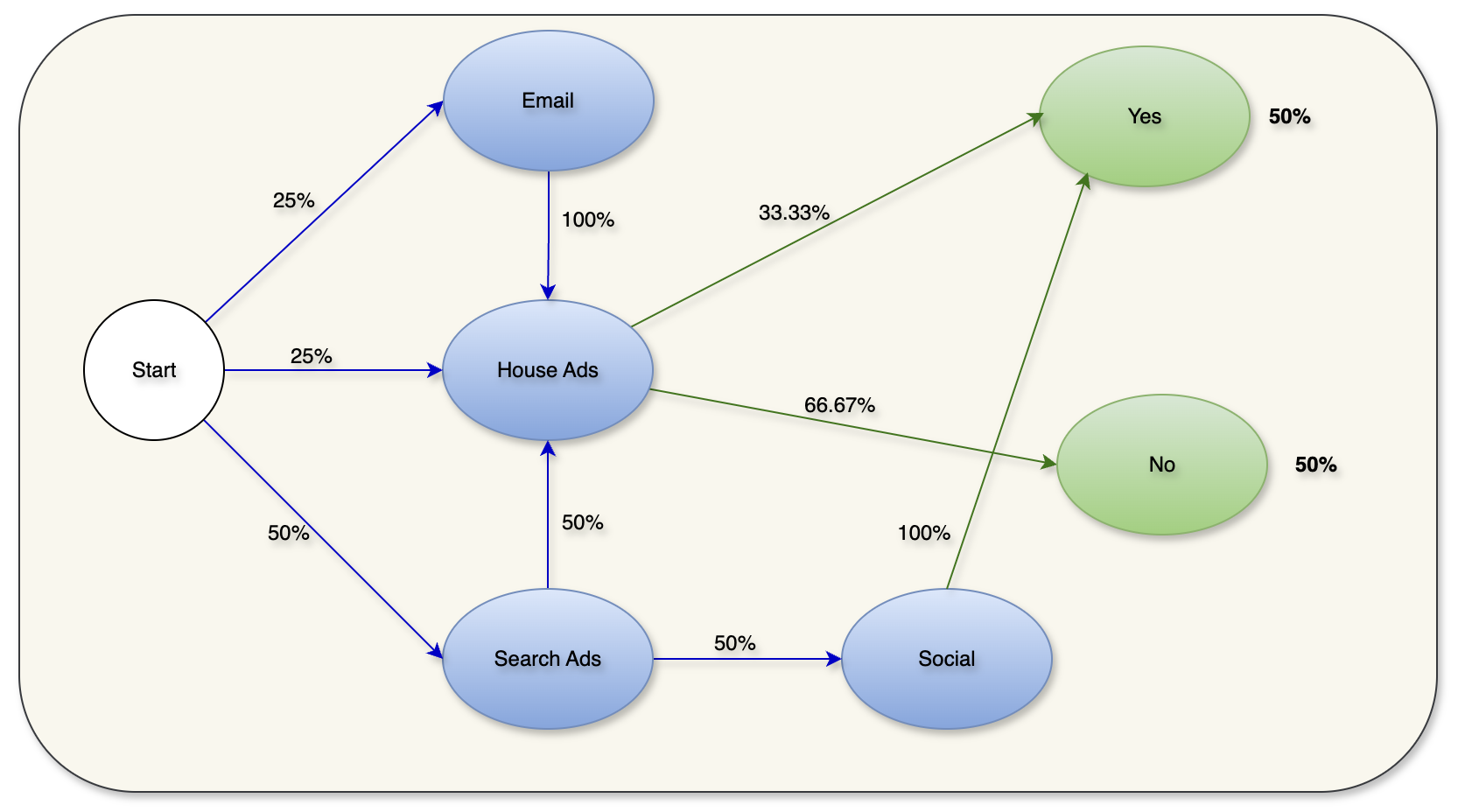
Rysunek 2: Customer Journey DAG
Efekt usunięcia
Ważnym aspektem atrybucji łańcucha Markowa jest to, w jaki sposób usunięcie danego punktu styku z wykresu wpływa na prawdopodobieństwo konwersji.
Proszę usunąć Email węzeł z powyższego wykresu, aby zrozumieć to zachowanie.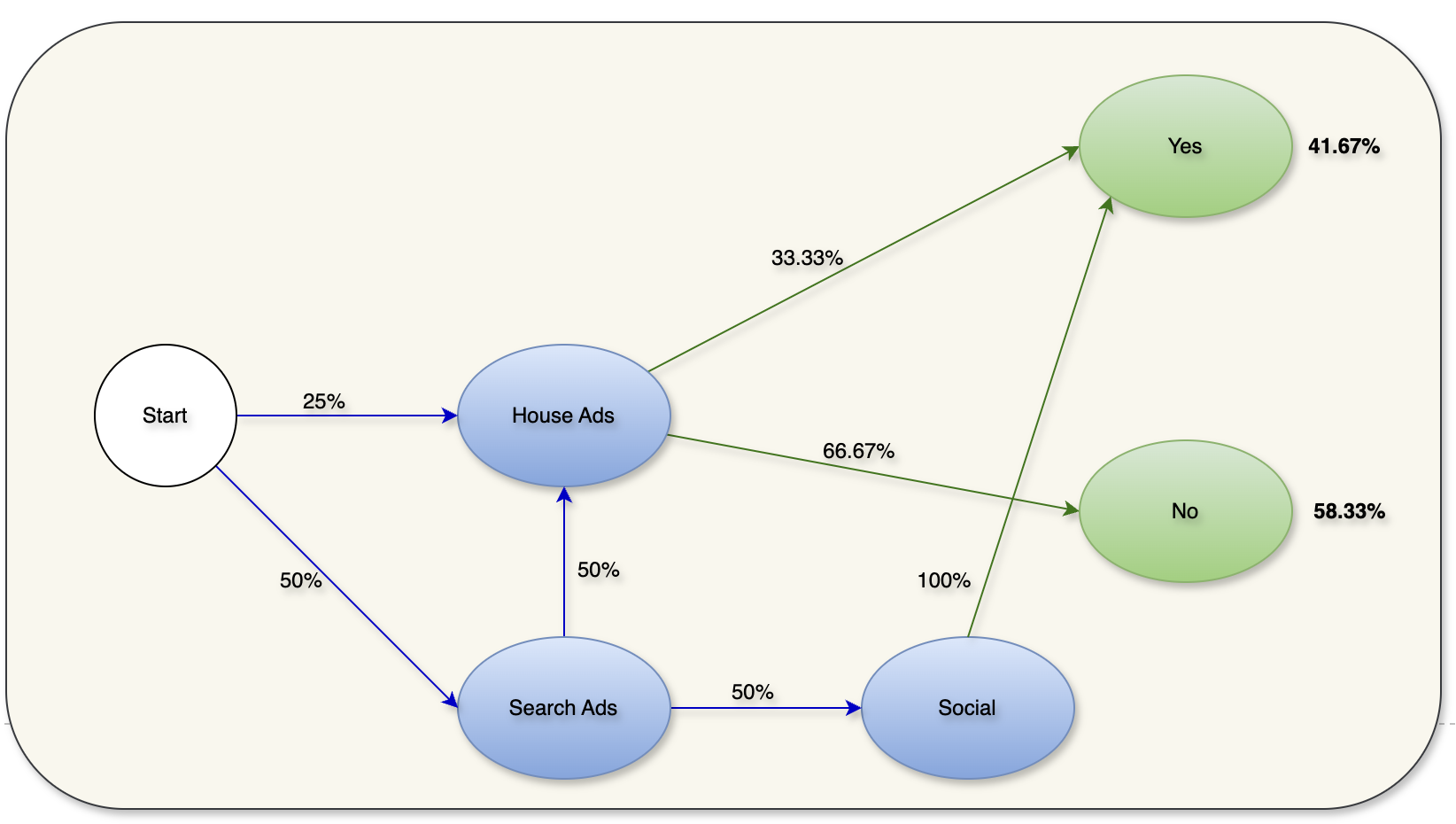
Rysunek 3: DAG z usuniętym węzłem Email
Po usunięciu wiadomości e-mail prawdopodobieństwo konwersji zmniejszyło się do 41,67% z 50%. Teraz efekt usunięcia kanału można obliczyć za pomocą poniższego wzoru:

W oparciu o powyższy wzór, prawdopodobieństwo konwersji dla Email można obliczyć jako:
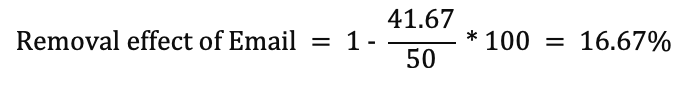
Podobnie, efekt usuwania innych kanałów można obliczyć za pomocą powyższego wzoru, a udział każdego kanału można obliczyć w następujący sposób:

| Kanał | Prawdopodobieństwo konwersji | Efekt usunięcia | Udostępnij |
| House Ads | 25% | 50% | 0.273 |
| Szukaj reklam | 16.67% | 66.67% | 0.364 |
| Społecznościowe | 25% | 50% | 0.273 |
| 41.67% | 16.67% | 0.090 |
Ograniczenia łańcucha Markowa
- Łańcuchy Markowa zakładają, że następny stan (lub punkt styku) zależy tylko od bieżącego stanu, a nie od historii stanów. Założenie to może nie odzwierciedlać dokładnie scenariuszy marketingowych, w których efekt punktu styku może zależeć od poprzednich interakcji.
- Model ten często pomija wpływ jednego kanału na skuteczność innego, potencjalnie nie doceniając efektów synergicznych lub tłumiących między różnymi kanałami marketingowymi.
- Modele łańcucha Markowa wymagają kompleksowych i szczegółowych danych na temat interakcji z klientami we wszystkich kanałach i punktach styku.
Model atrybucji wartości Shapleya
Model wartości Shapleya, wywodzący się z teorii gier kooperacyjnych, oferuje unikalne i sprawiedliwe podejście do MTA w marketingu. Przypisuje on wartość każdemu punktowi styku w sposób, który sprawiedliwie odzwierciedla jego wkład w ogólny sukces kampanii marketingowej. Jego celem jest sprawiedliwa metoda atrybucji, która uwzględnia wszystkie możliwe kombinacje punktów styku, zapewniając, że każdy z nich otrzyma kredyt proporcjonalny do jego wpływu.
Koncepcja i kontekst
Opracowana przez Lloyda Shapleya w 1953 roku wartość Shapleya jest koncepcją rozwiązania w teorii gier kooperacyjnych. Ma ona na celu sprawiedliwy podział zysków między graczy, którzy współpracują i wnoszą różny wkład do koalicji. W scenariuszu gry kooperacyjnej, w której wielu graczy łączy siły w celu stworzenia koalicji, zwiększając tym samym szanse na pomyślny wynik (lub wypłatę), wartość Shapleya oferuje metodę sprawiedliwego podziału wypłaty między uczestników.
Wartość Shapleya oblicza średni wkład każdego gracza w koalicje, w których uczestniczy. Obliczenia te uwzględniają zmienność wpływu (lub wartości) każdego gracza i kolejność, w jakiej dołączają do koalicji, biorąc pod uwagę, że każda sekwencja dołączania ma równe szanse na wystąpienie. Dlatego gracze są wynagradzani na podstawie ich wkładu we wszystkich możliwych permutacjach. W przypadku zastosowania do analityki marketingowej, graczami w tym scenariuszu są różne kanały kampanii, a koalicje reprezentują różne sposoby interakcji i interakcji tych kanałów z kontami podczas podróży klienta. Wykorzystując teorię gier kooperacyjnych i wartość Shapleya, możemy osiągnąć stabilną i sprawiedliwą miarę wpływu każdego kanału, przydzielając im kredyt za konwersje sprzedaży proporcjonalnie do ich indywidualnego wkładu w ogólny wynik.
Podejście algorytmiczne
- Proszę wyliczyć wszystkie możliwe koalicje: Proszę wymienić wszystkie możliwe kombinacje (podzbiory) punktów styku, które mogą prowadzić do konwersji.
- Proszę obliczyć wypłatę dla każdej koalicji: Proszę określić wartość (np. współczynnik konwersji), jaką osiąga każdy podzbiór punktów styku.
- Dystrybucja wartości między punktami styku: Dla każdego punktu styku należy obliczyć jego wkład we wszystkie możliwe koalicje, których jest częścią, w oparciu o różnicę, jaką wnosi do wartości koalicji.
Wartość Shapleya dla punktu styku jest obliczana przy użyciu wzoru:
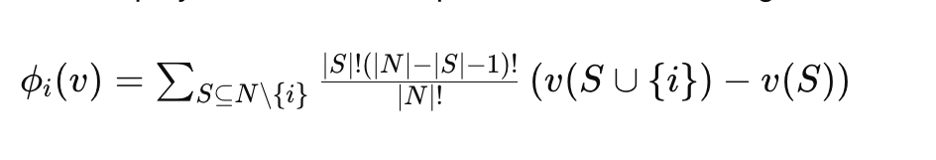
Gdzie:
- ϕi(v) jest wartością Shapleya dla punktu styku i.
- N to zbiór wszystkich punktów styku.
- S jest podzbiorem punktów styku z wyłączeniem i.
- v(S) jest wypłatą (wartością) podzbioru S.
- Suma obejmuje wszystkie podzbiory S of N które nie zawierają i.
Weźmy przykład punktów styku zaangażowanych w konwersję:
- N = { Search Ads, Social, Email }
Poniżej przedstawiono stosunek każdej koalicji do konwersji:
| Koalicja | Kanały | Stosunek |
| S1 | 0.04 | |
| S2 | Ogłoszenia wyszukiwania | 0.12 |
| S3 | Social | 0.08 |
| S4 | Email + Search Ads | 0.17 |
| S5 | Social + Search Ads | 0.22 |
| S6 | Email + Social | 0.11 |
| S7 | Search + Social + House Ads | 0.26 |
The wypłata lub warto każdej koalicji jest określana przez funkcję charakterystyczną. W tym przykładzie wartość jest reprezentowana jako suma współczynnika konwersji każdego kanału w koalicji.
Aby znaleźć wartość wypłaty koalicji S5, proszę użyć:
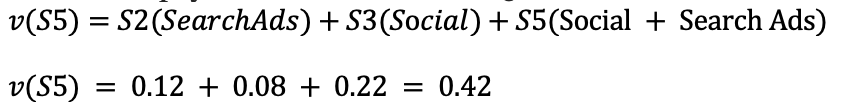
Tak więc wypłatę każdej koalicji można obliczyć jak pokazano poniżej:
| Funkcja | Kanały | Obliczenia | Wypłata |
| v(S1) | S1 | 0.04 | |
| v(S2) | Reklamy w wyszukiwarce | S2 | 0.12 |
| v(S3) | Social | S3 | 0.08 |
| v(S4) | E-mail + reklamy w wyszukiwarce | S1 + S2 + S4 | 0.33 |
| v(S5) | Social + Search Ads | S2 + S3 + S5 | 0.42 |
| v(S6) | Email + Social | S1 + S3 + S6 | 0.23 |
| v(S7) | Search + Social + House Ads | S1+ S2 + S3 + S4 + S5 + S6 | 1.0 |
Zrozumienie wartości wnoszonej przez każdą koalicję pozwala na obliczenie wartości Shapleya. Są one określane poprzez uśrednienie przyrostowego wkładu (wkładu krańcowego) każdego kanału we wszystkich możliwych sekwencjach tworzenia koalicji. Zasadniczo metoda wartości Shapleya oferuje systematyczne podejście do podziału całkowitej wartości wygenerowanej przez wielką koalicję (zbiorowa wypłata) między trzy kanały. Podejście to zapewnia sprawiedliwą dystrybucję w oparciu o unikalny wkład każdego kanału w ogólny wynik.
Rzeczywiście, motywacja stojąca za sformułowaniem wartości Shapleya polega na uwzględnieniu konkretnego momentu, w którym każdy kanał lub punkt styku dołącza do koalicji. Czas ten ma kluczowe znaczenie, ponieważ wpływa na marginalny wkład gracza w ogólny wynik. Zasadniczo metoda Shapley Value polega na obliczeniu przyrostowego wkładu każdego kanału, uśrednionego dla wszystkich potencjalnych sekwencji, w których kanał lub punkt kontaktowy może dołączyć do grupy. Jeśli kanał lub punkt styku pojawia się jako pierwszy, jego indywidualna wypłata jest uważana za marginalny wkład, jeśli pojawia się później w kolejności, jego podzbiór koalicji obejmujący wcześniejsze punkty styku w sekwencji minus ten bez bieżącego kanału lub punktu styku byłby uważany za jego marginalny wkład w koalicję. Wartość Shapleya to średni oczekiwany wkład krańcowy jednego kanału lub punktu styku po uwzględnieniu wszystkich możliwych kombinacji.
W opisanym przez Pana scenariuszu wymaga to symulacji każdej możliwej kolejności, w jakiej punkty styku (Email, Społeczne, oraz Szukaj reklam) mogą nawiązać kontakt z klientem. Dla każdej z tych sekwencji należy oszacować dodatkową wartość (krańcową wypłatę) przynoszoną przez każdy punkt styku po dodaniu go do sekwencji. Następnie, uśredniając te przyrostowe wartości we wszystkich sekwencjach, uzyskuje się wartość Shapleya dla każdego punktu styku.
Metoda ta zapewnia uczciwą i kompleksową ocenę wkładu każdego punktu styku, biorąc pod uwagę każdy możliwy sposób interakcji w podróży klienta, odzwierciedlając w ten sposób ich prawdziwą wartość w wielkim schemacie strategii marketingowej.
Rozważmy wielką koalicję S7 i znajdźmy wartość Shapleya, aby rozdzielić wypłatę na każdy kanał w oparciu o kolejność przybycia każdego kanału.
| Arrival Order | Email Marginal Contribution | Marginalny wkład społeczny | Marginalny wkład reklam w wyszukiwarce |
| Email + Social + Search | v(S1) = 0.04 | v(S6) – v(S1) = 0.19 | v(S7 ) – v(S6) = 0.77 |
| Email + Search + Social | v(S1) = 0.04 | v(S7 ) – v(S4) = 0,67 | v(S4) – v(S1) = 0,29 |
| Social + Email + Search | v(S6) – v(S3) = 0,15 | v(S3) = 0.08 | v(S7 ) – v(S6) = 0,77 |
| Social + Search + Email | V(S7) – v(S5) = 0,58 | v(S3) = 0,08 | v(S5) – v(S2) = 0,30 |
| Search + Email + Social | v(S4) – v(S2) = 0,11 | v(S7 ) – v(S4) = 0,67 | v(S2) = 0,12 |
| Search + Social + Email | v(S7) – v(S5) = 0,58 | v(S5) – v(S2) = 0,30 | v(S2) = 0.12 |
| Wartość Shapleya lub Średnia krańcowa Wkład |
0.25 | 0.332 | 0.395 |
Ograniczenia wartości Shapleya
- Obliczanie wartości Shapleya może być kosztowne obliczeniowo, zwłaszcza w przypadku dużej liczby graczy (lub kanałów marketingowych). Model wymaga oceny każdej możliwej kombinacji graczy, która rośnie wykładniczo wraz z liczbą graczy.
- Gdy brakuje bezpośrednich informacji o konkretnych koalicjach, można wykorzystać dostępne dane do oszacowania ich wartości. Można to zrobić za pomocą modelowania statystycznego, technik uczenia maszynowego lub nawet prostszych metod heurystycznych.
Bayesowskie modele prawdopodobieństwa
Bayesian Attribution Model to zaawansowane podejście w dziedzinie MTA, które wykorzystuje statystyki bayesowskie do wnioskowania o wpływie różnych marketingowych punktów styku na zachowania konsumentów i współczynniki konwersji. Model ten jest szczególnie godny uwagi ze względu na jego zdolność do radzenia sobie z niepewnością i integrowania wcześniejszej wiedzy z ramami analitycznymi.
Koncepcja i funkcjonalność
Atrybucja bayesowska jest zakorzeniona w Prawdopodobieństwo bayesowskie, które aktualizuje oszacowanie prawdopodobieństwa hipotezy w miarę pojawiania się nowych dowodów lub informacji. Podejście to jest szczególnie przydatne w sytuacjach, w których dane są niekompletne lub niepewne. W kontekście MTA model bayesowski ocenia prawdopodobieństwo konwersji, biorąc pod uwagę ekspozycję na różne marketingowe punkty styku. Aktualizuje te prawdopodobieństwa w miarę udostępniania nowych danych, dzięki czemu jest to dynamiczny i stale ewoluujący model.
Podejście algorytmiczne
- Definiowanie wcześniejszych prawdopodobieństw: Proszę zacząć od wstępnych założeń lub “priorytetów” dotyczących skuteczności różnych punktów styku. Założenia te mogą być oparte na danych historycznych lub opiniach ekspertów. W przypadku braku wcześniejszych danych można zastosować jednolity rozkład prawdopodobieństwa lub inne metody statystyczne. Załóżmy, że mamy wcześniejsze przekonania (oparte na danych historycznych lub opiniach ekspertów) na temat skuteczności każdego kanału
- Zbieranie danych: Zbieranie danych na temat interakcji klientów z różnymi punktami styku na ich drodze do konwersji.
- Aktualizacja prawdopodobieństwa: W miarę pojawiania się nowych danych, model aktualizuje prawdopodobieństwa przy użyciu twierdzenia Bayesa. Twierdzenie to łączy wcześniejsze prawdopodobieństwa z nowymi dowodami w celu uzyskania zaktualizowanych (późniejszych) prawdopodobieństw.
- Ciągłe uczenie się: Model stale aktualizuje swoje zrozumienie skuteczności punktu styku w miarę gromadzenia większej ilości danych dotyczących interakcji, udoskonalając swoje spostrzeżenia w czasie.
Atrybucja bayesowska wykorzystuje twierdzenie Bayesa, które w swojej podstawowej formie brzmi:
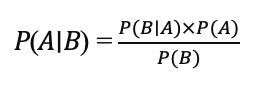
Gdzie:
- P(A∣B) jest prawdopodobieństwem następczym (np. prawdopodobieństwo konwersji przy ekspozycji na określony punkt styku).
- P(B∣A) to prawdopodobieństwo (np. prawdopodobieństwo zaobserwowania danych, biorąc pod uwagę skuteczność punktu styku).
- P(A) to wcześniejsze prawdopodobieństwo (początkowe założenie dotyczące skuteczności punktu styku).
- P(B) jest prawdopodobieństwem krańcowym danych.
Przeanalizujmy Bayesian Multi-Touch Attribution w przykładzie podróży klienta obejmującym Reklamy displayowe, Szukaj reklam, Media społecznościowe, oraz Email Ads. Załóżmy, że mamy wcześniejsze przekonania (oparte na danych historycznych lub opiniach ekspertów) na temat skuteczności każdego kanału.
| Kanał | Wcześniejsze prawdopodobieństwo |
| Reklamy displayowe (A) | 0.35 |
| Reklamy w wyszukiwarce (B) | 0.30 |
| Social (C) | 0.25 |
| Email (D) | 0.10 |
Proszę obliczyć prawdopodobieństwo na podstawie punktów danych. Na przykład, jeśli 70% konwersji obejmuje Reklamy w wyszukiwarce w podróży, to prawdopodobieństwo, że Reklamy w wyszukiwarce wynosi 0,7.
| Kanał | Prawdopodobieństwo |
| Reklamy displayowe (A) | 0.75 |
| Reklamy w wyszukiwarce (B) | 0.70 |
| Social (C) | 0.50 |
| Email (D) | 0.35 |
- Prawdopodobieństwo krańcowe = Suma(Prawdopodobieństwo kanału i X Uprzednie prawdopodobieństwo kanału i); dla każdego kanału
- Prawdopodobieństwo krańcowe na podstawie powyższych danych = (0,75*0,35) + (0,7*0,3) + (0,5*0,25) + (0,35*0,1) = 0.633
Korzystając z twierdzenia Bayesa, można obliczyć prawdopodobieństwo następcze:
| Kanał | Posterior Probability |
| Reklamy displayowe (A) | (0.75*035/0.633) = 0.42 |
| Reklamy w wyszukiwarce (B) | (0.7*0.3)/0.633 = 0.33 |
| Społeczne (C) | (0.5*0.25)/0.633 = 0.20 |
| Email (D) | (0.35*0.10)/0.633 = 0.05 |
Ograniczenia
Dokładność modelu jest częściowo zależna od wcześniejszych prawdopodobieństw przypisanych do skuteczności różnych kanałów. Te priorytety mogą być subiektywne i mogą wypaczyć model, jeśli nie zostaną dokładnie ustawione.
Modele atrybucji oparte na uczeniu maszynowym
Uczenie maszynowe modele obejmują modele regresji, drzewa decyzyjne, lasy losowe i sieci neuronowe. Modele te analizują złożone interakcje między punktami styku i mogą obsługiwać różne typy danych, w tym dane nieustrukturyzowane. Potrafią obsługiwać duże zbiory danych i znajdować nieliniowe relacje. Dostosowują się, gdy nowe dane stają się dostępne, zapewniając stale udoskonalane spostrzeżenia. Algorytmy uczenia maszynowego (ML) znacznie rozwinęły dziedzinę MTA, wprowadzając wyrafinowane metody analizy złożonych podróży klientów. Algorytmy te mogą rozszyfrować skomplikowane wzorce w dużych zbiorach danych, umożliwiając marketerom dokładniejsze zrozumienie i przypisanie wpływu różnych punktów styku.
Koncepcja i zastosowanie
Algorytmy ML w MTA wykorzystują podejścia oparte na danych do modelowania i przewidywania wpływu każdego marketingowego punktu styku na ścieżkę konwersji klienta. Wykraczają one poza tradycyjne modele atrybucji oparte na regułach, ucząc się na podstawie danych w celu określenia, w jaki sposób różne punkty styku przyczyniają się do konwersji. Algorytmy ML są wykorzystywane do analizy podróży klienta w wielu kanałach i punktach styku. Mogą one obsługiwać rozległe i zróżnicowane zbiory danych, uwzględniając nieliniowe relacje i interakcje między punktami styku.
Rodzaje algorytmów uczenia maszynowego
- Uczenie nadzorowane:
- Koncepcja: Uczenie nadzorowane polega na trenowaniu modelu na oznaczonym zbiorze danych, w którym znane są dane wejściowe (cechy) i pożądane dane wyjściowe (etykiety). Model uczy się mapować dane wejściowe na dane wyjściowe.
- Popularne algorytmy: Modele regresji, drzewa decyzyjne, lasy losowe, maszyny wektorów nośnych i sieci neuronowe.
2. Uczenie bez nadzoru:
- Koncepcja: Nienadzorowane uczenie się znajduje wzorce lub struktury w zbiorze danych bez wcześniej istniejących etykiet. Algorytmy odkrywają nieodłączne grupy lub powiązania w danych.
- Przykłady: Algorytmy grupowania, takie jak K-średnich, hierarchiczne grupowanie i analiza głównych składowych (PCA).
Wnioski
Atrybucja Multi-Touch (MTA) stała się kluczowym narzędziem w nowoczesnej analityce marketingowej, oferując wyrafinowany sposób zrozumienia i ilościowego określenia wpływu różnych punktów styku w podróży klienta. Wykraczając poza ograniczenia tradycyjnych modeli atrybucji pojedynczego dotknięcia, MTA zapewnia bardziej zniuansowany i kompleksowy obraz skuteczności różnych kanałów i strategii marketingowych.
Jego zdolność do dokładniejszego podziału kredytów za konwersje w wielu interakcjach pomaga marketerom optymalizować ich kampanie, efektywnie alokować budżety i skuteczniej dostosowywać doświadczenia klientów. Jednak złożoność i intensywny charakter danych modeli MTA, wraz z potrzebą zaawansowanych umiejętności analitycznych, oznaczają, że ich wdrożenie może stanowić wyzwanie. Pomimo tych wyzwań, spostrzeżenia uzyskane dzięki MTA są nieocenione dla firm, które chcą poruszać się po złożonym, wielokanałowym krajobrazie nowoczesnego marketingu cyfrowego.
Wraz z postępem technologicznym i coraz większą dostępnością danych, MTA prawdopodobnie stanie się jeszcze bardziej integralną częścią skutecznego rozwoju i oceny strategii marketingowej.
Referencje
- Kakalejčík, L., Bucko, J., Resende, P.A. i Ferencova, M., 2018. Atrybucja marketingu wielokanałowego z wykorzystaniem łańcuchów Markowa. Journal of Applied Management and Investments, 7(1), pp.49-60.
- Zhao, K., Mahboobi, S.H. i Bagheri, S.R., 2018. Metody wartości Shapleya do modelowania atrybucji w reklamie internetowej. arXiv preprint arXiv:1804.05327.
- Sinha, R., Arbour, D. i Puli, A.M., 2022. Modelowanie bayesowskie atrybucji marketingowej. arXiv preprint arXiv:2205.15965.
- Berman, R., 2018. Beyond the last touch: Atrybucja w reklamie internetowej. Marketing Science, 37(5), pp.771-792.
- Romero Leguina, J., Cuevas Rumín, Á. i Cuevas Rumín, R., 2020. Atrybucja marketingu cyfrowego: Zrozumienie ścieżki użytkownika. Elektronika, 9(11), p.1822.
- Jedna metoda przypisywania cech (rzekomo) rządzi wszystkimi: wartości Shapleya
- Atrybucja marketingowa oparta na danych
- Modelowanie atrybucji w oparciu o łańcuch Markowa [Complete Guide]
- Modelowanie atrybucji łańcucha Markowa [Complete Guide]
